This project conducted since 2009 aims to develop methods allowing the inclusion of nuclear quantum effects in simulations using the molecular dynamics method (MD). Indeed, the use of molecular dynamics (MD) for the simulation of material properties is limited to temperatures above Debye's temperature, since it is based on classical mechanics. The MD method, therefore cannot quantitatively predict physical properties at low temperatures (below a few hundred Kelvin).
To include quantum effects in the standard molecular dynamics (MD), several techniques have been developed. The most well-known method is the PIMD (Path Integral Molecular Dynamics) which is based on the path integrals developed by Feynman. This method, simple to implement, is very time-consuming to calculate. Moreover, it does not allow to obtain directly the time correlations of the quantities.
An approximate method has been developed that can take into account quantum effects without significantly increasing computation time. The QTB (Quantum Thermal Bath) method that we published in 2009, is based on a so-called harmonic approximation and uses a Langevin-type dynamic through a spectral power density of the random force that depends on frequency. For highly anharmonic systems, we have combined the QTB method with the PIMD method to accelerate its convergence and significantly reduce computation time.
To be able to calculate time correlations, other methods such as CMD (centroid molecular dynamics) or RPMD (ring polymer molecular dynamics) have been developed. The purpose of the present work is to adapt one of this two methods to include QTB in order to benefit from the gain in computation time thanks to QTB.
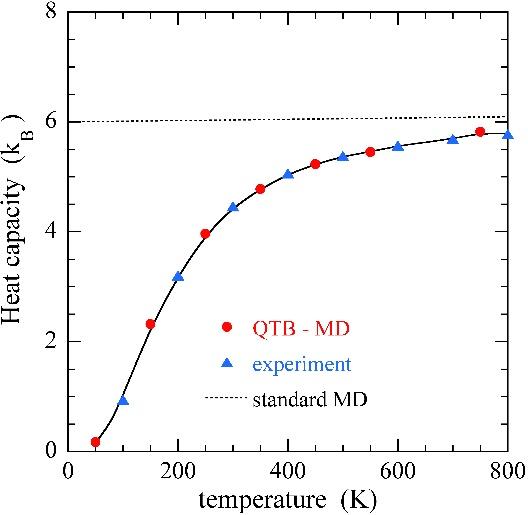
Figure 1: Heat capacity of MgO crystal calculated by the QTB-MD method (H. Dammak et al. Phys. Rev. Lett. 103 (2009) 190601)

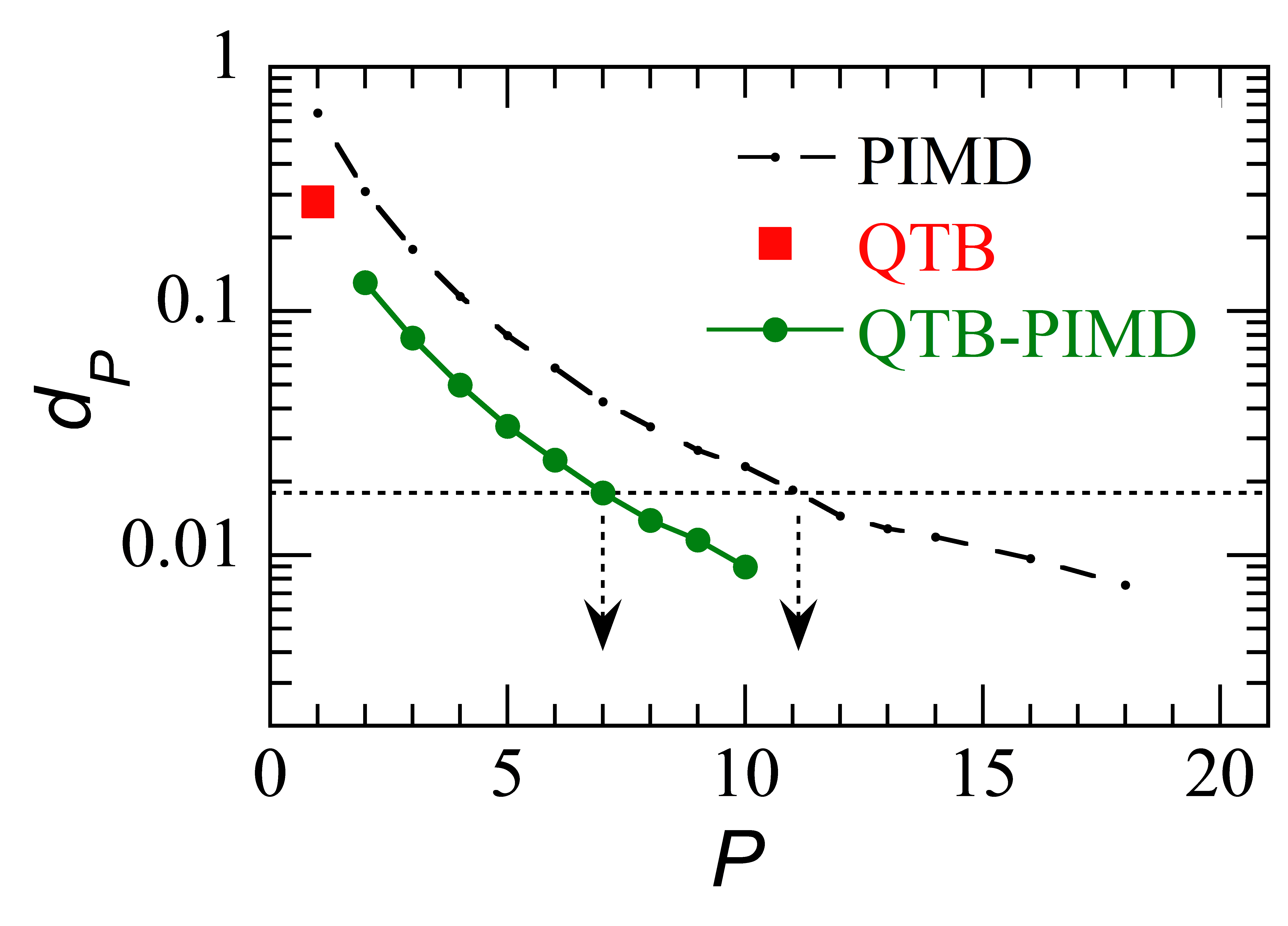
Figure 2: Top: position distribution of a proton in a double-well at ?=0,4 obtained by QTB-PIMD (P = 6, green), PIMD (P = 11, blue) and QTB (red). Bottom: Divergence factor as a function of the number of replicas, P. (F. Brieuc et al. J. Chem. Theory Comput. 12 (2016) 1351)

